How the Fermi Thread Block Scheduler Works (Illustrated)
Table of Contents
1 Introduction
The Fermi Thread Block Scheduler (TBS) is a hardware scheduler on the GPU that dispatches a CUDA kernel's thread blocks to the GPU's streaming multiprocessors (SMs). It is widely believed that both thread blocks and SMs are scheduled using a round-robin algorithm. However, experimental data does not support this belief.
For example, here is an execution timeline of a 4x4 grid with maximum residency of one thread block on a 14-SM Quadro 6000. The y-axis reports the value of %smid register which contains the SM identifier, while the x-axis represents time. Each horizontal bar represents a thread block with TBx indicating the thread block's linear ID.
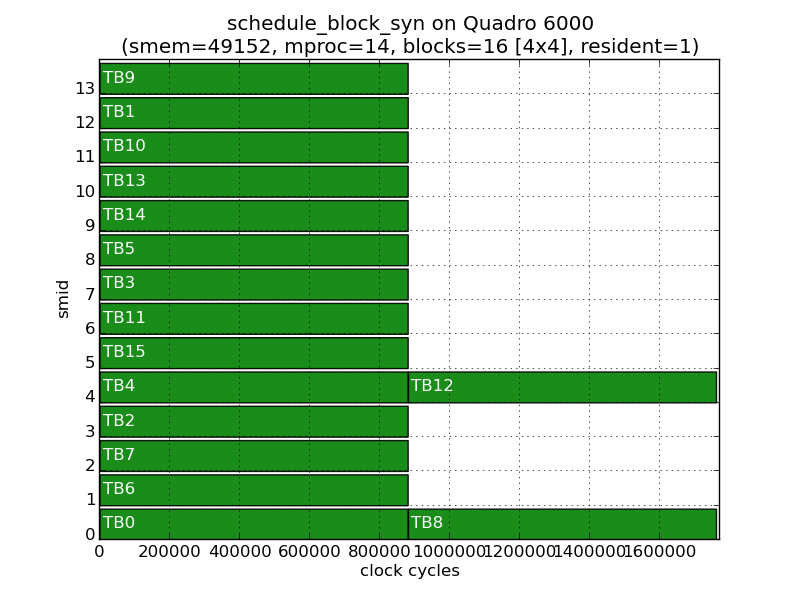
As the residency is 1 and there are only 14 SMs, two blocks must wait for execution. Curiously, it is thread blocks 8 and 12 that end up waiting and not thread blocks 14 and 15 as we might expect.
In this document, I show that the TBS uses a mostly round-robin technique to pick SMs, but a far more interesting way to pick thread blocks. The algorithms described in this document were arrived at by looking at block IDs, %smid register values and clock64() values. They do not necessarily reflect how the Fermi TBS is actually implemented in the hardware. However, they exactly match TBS behaviour on the Quadro 6000, the GTX 480 and the Tesla C2070, all of which use the GF100 Fermi GPU in varying configurations.
2 Fermi Hardware Basics
The NVIDIA Fermi (GF100) is a Compute Capability 2.0 GPU. Fermi-based GPUs can contain up to 16 SMs, organized into Graphics Processor Clusters (GPCs) containing up to 4 SMs each. The cards that I experiment on, the Quadro 6000 and the Tesla C2070, contain only 14 SMs, with two GPCs containing 3 SMs each. I have also tested against a GeForce GTX 480, another Fermi-based GPU, but containing 15 SMs so that only one GPC has 3 SMs.
For the Quadro 6000 under experimentation, we have the following correspondence of SMs to GPCs:
- GPC0: {SM0, SM4, SM8, SM12}
- GPC1: {SM1, SM5, SM9}
- GPC2: {SM2, SM6, SM10}
- GPC3: {SM3, SM7, SM11, SM13}
This correspondence was worked out from clock64() values as well as in hindsight with knowledge of the scheduling algorithm.
3 Summary of the Fermi Scheduler
The Fermi TBS takes the following attributes of a grid into account when scheduling: number of thread blocks, its maximum residency on an SM and its shape (1-D or 2-D). The first two attributes control the order in which SMs are picked while the last attribute controls the order in which thread blocks are picked. The scheduler only picks SMs for the first wave of thread blocks which contains (number of SMs * maximum residency) thread blocks, not necessarily consecutive.
Simply put, the Fermi TBS picks GPCs in almost round-robin order. The "almost" caveat applies because the Fermi prioritizes GPCs that can run more thread blocks because they contain more SMs. Once a GPC has been picked, depending on the number of thread blocks remaining to be scheduled, the TBS either dispatches thread blocks to all SMs in that GPC or one thread block to a SM in a GPC. When dispatching one thread block to a GPC, the target SM is always picked in strict round-robin order of %smid. The objective seems to be to spread the thread blocks across the entire GPU to minimize load imbalance. After the initial wave, SMs are picked in the order of completing thread blocks.
The shape of a grid (1-D or 2-D) influences the order in which thread blocks are picked. For 1-D grids, thread blocks are picked in increasing order of thread block ID. For 2-D grids, thread blocks are picked in a pattern resembling a space-filling Hilbert curve aimed perhaps at preserving 2-D locality. I have not experimented with 3-D grids that became available with CUDA 4.0 onwards.
The overall operation can be described by the pseudo-code below:
total_blocks = grid.sizeX * grid.sizeY
initial_blocks = min(total_blocks, grid.residency * gpu.number_of_sm)
while initial_blocks-- > 0:
sm = pick_sm()
block = pick_block()
schedule block to sm
total_blocks -= initial_blocks
while total_blocks > 0:
block = pick_block()
wait for a thread block to finish on any SM
schedule block to that SM
The rest of this document explains how `pick_sm()` and `pick_block()` work presenting experimental data that was used to deduce their functioning.
4 Computing the Initial Mapping
As stated earlier, `pick_sm()` applied only to an initial set of thread blocks containing number of SMs * maximum residency thread blocks. This set does not necessarily contain consecutive thread blocks. After this set has been scheduled, thread blocks continue to be picked in the order
4.1 pick_sm()
The following figure shows the execution of a one-dimensional grid of 28 thread blocks with a residency of 2. Therefore, the initial set contains all the 28 thread blocks. As before, each horizontal bar represents one thread block, but now shows the value of %smid inside, while the thread block ID is shown on the y-axis.
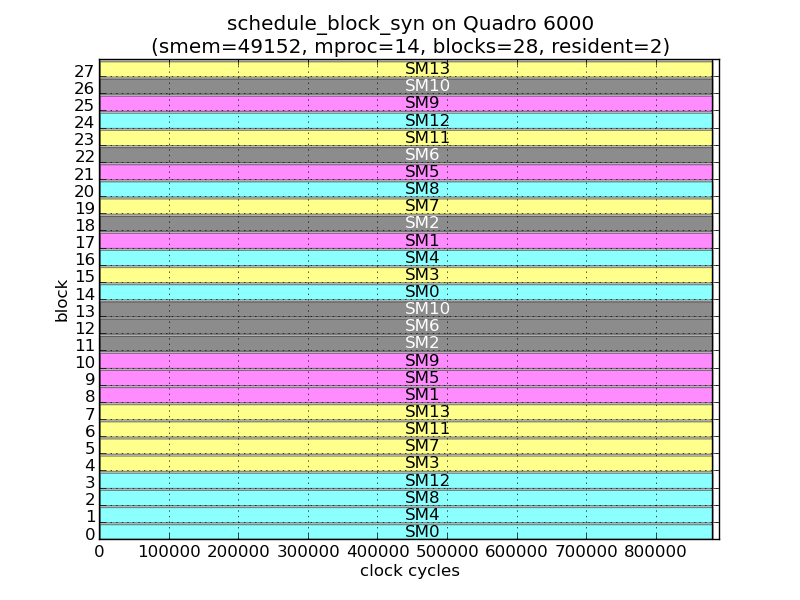
For the first 14 blocks in this 28-block grid, the TBS dispatches 4 (or 3) blocks to each GPC initially. Viewed in order of block ID, the TBS prioritizes GPCs with 4 SMs over those that contain 3 SMs. So blocks 0–3 execute on GPC0, blocks 4–7 on GPC3, blocks 8–10 on GPC1 and blocks 11–13 on GPC2. Within each GPC, the blocks are assigned to each SM in a round-robin order.
For the remaining 14 blocks in the initial set, the TBS dispatches one thread block at a time to each GPC. So TB14 goes to SM0 in GPC0, TB15 goes to SM3 in GPC3, TB16 goes back to GPC0, but to SM4, and so on.
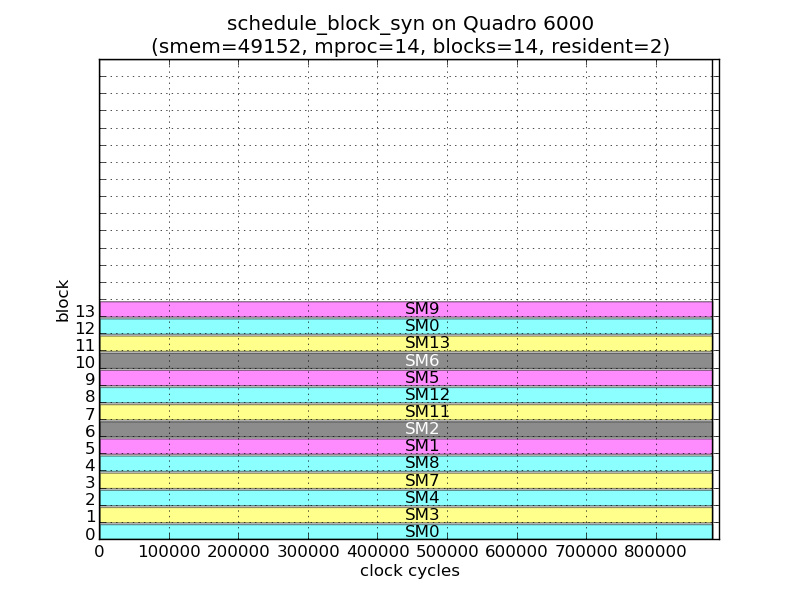
This establishes that the TBS dispatches blocks to all SMs or one SM in each GPC. Further, each GPC is picked in some priority order with SMs in that GPC chosen in round-robin order of %smid. This second fact is reinforced by the next figure which shows the timeline of a 14-block, residency 2 grid. In this figure, thread blocks are being dispatched one-at-a-time from the start, and GPC0 and GPC3 are chosen thrice and twice respectively before the scheduler even chooses GPC1.
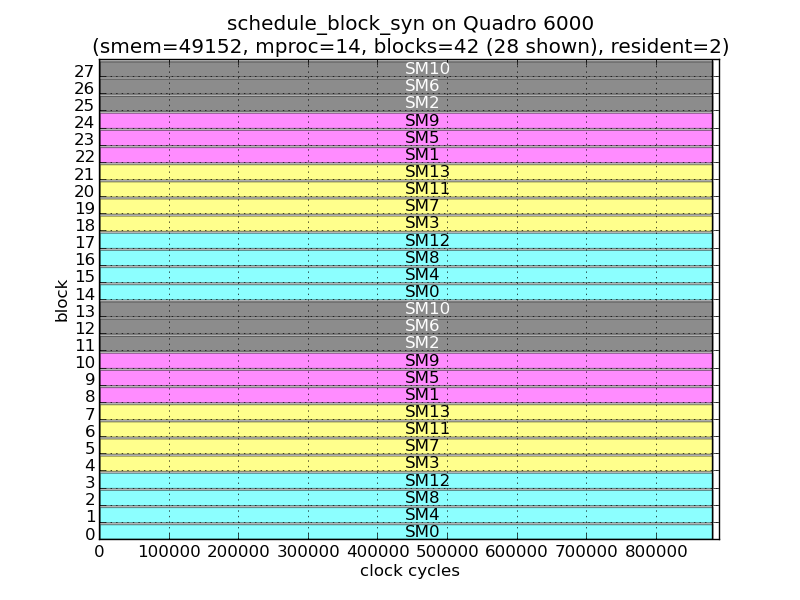
Although the previous two figures suggest that the TBS switches to dispatching thread blocks one-at-a-time when there are less than 14 thread blocks remaining, the following figure showing the execution of a 42x1 grid at residency 2 shows that the switch happens only when there are less than 14 thread blocks remaining overall. The choice of 14 seems to be simply the number of SMs in the Quadro 6000.
All that remains now is to determine how priorities are assigned to each GPC, and that turns out simply to be the residency of the grid multiplied by the number of SMs in that GPC. For the Quadro 6000, a grid of residency 2 would have the initial set of priorities:
priorities = [4*2, 3*2, 3*2, 4*2] = [8, 6, 6, 8]
The next GPC to be picked is then given by:
max_prio = max(priorities) max_cluster = priorities.index(max_prio) priorities[max_cluster] -= blocks_dispatched
where priorities.index returns the lowest indexed GPC with priority == max_prio. Once selected, the priority for a cluster is then reduced by the number of thread blocks dispatched to it.
The following table illustrates the scheduling of a 28x1 grid of residency 2 in detail:
| Order | Block ID | %smid | Cluster | SM (calc) | SM Cluster | Priority |
| 0 | 0 | 0 | 0 | 0 | 0 | 8 |
| 1 | 1 | 4 | 0 | 4 | 0 | 8 |
| 2 | 2 | 8 | 0 | 8 | 0 | 8 |
| 3 | 3 | 12 | 0 | 12 | 0 | 8 |
| 4 | 4 | 3 | 3 | 3 | 3 | 8 |
| 5 | 5 | 7 | 3 | 7 | 3 | 8 |
| 6 | 6 | 11 | 3 | 11 | 3 | 8 |
| 7 | 7 | 13 | 3 | 13 | 3 | 8 |
| 8 | 8 | 1 | 1 | 1 | 1 | 6 |
| 9 | 9 | 5 | 1 | 5 | 1 | 6 |
| 10 | 10 | 9 | 1 | 9 | 1 | 6 |
| 11 | 11 | 2 | 2 | 2 | 2 | 6 |
| 12 | 12 | 6 | 2 | 6 | 2 | 6 |
| 13 | 13 | 10 | 2 | 10 | 2 | 6 |
| 14 | 14 | 0 | 0 | 0 | 0 | 4 |
| 15 | 15 | 3 | 3 | 3 | 3 | 4 |
| 16 | 16 | 4 | 0 | 4 | 0 | 3 |
| 17 | 17 | 1 | 1 | 1 | 1 | 3 |
| 18 | 18 | 2 | 2 | 2 | 2 | 3 |
| 19 | 19 | 7 | 3 | 7 | 3 | 3 |
| 20 | 20 | 8 | 0 | 8 | 0 | 2 |
| 21 | 21 | 5 | 1 | 5 | 1 | 2 |
| 22 | 22 | 6 | 2 | 6 | 2 | 2 |
| 23 | 23 | 11 | 3 | 11 | 3 | 2 |
| 24 | 24 | 12 | 0 | 12 | 0 | 1 |
| 25 | 25 | 9 | 1 | 9 | 1 | 1 |
| 26 | 26 | 10 | 2 | 10 | 2 | 1 |
| 27 | 27 | 13 | 3 | 13 | 3 | 1 |
4.2 pick_blocks()
While the above description suffices to schedule all 1-D grids, the following figures show that the TBS also takes into account the shape of the grid when scheduling. These figures are from the executions of grids containing 12 thread blocks, but with different shapes: 12x1, 2x6, 3x4, 4x3 and 6x2.
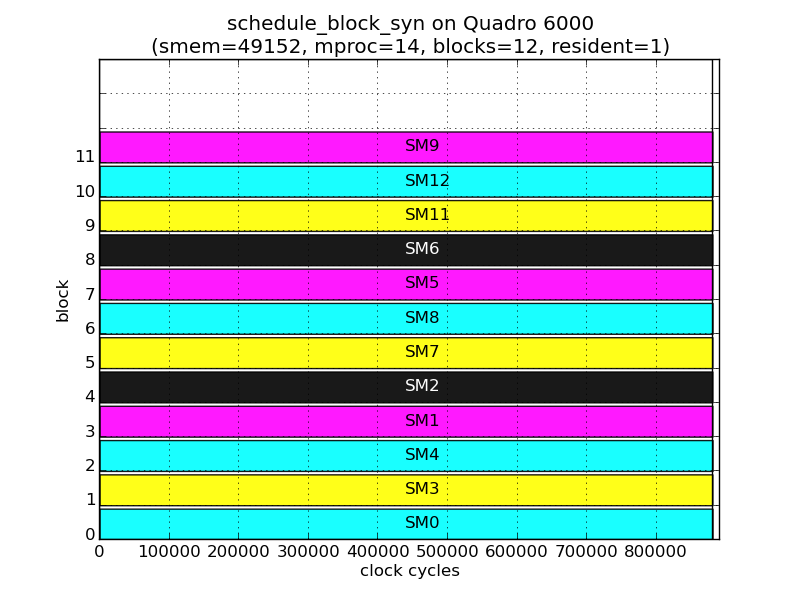
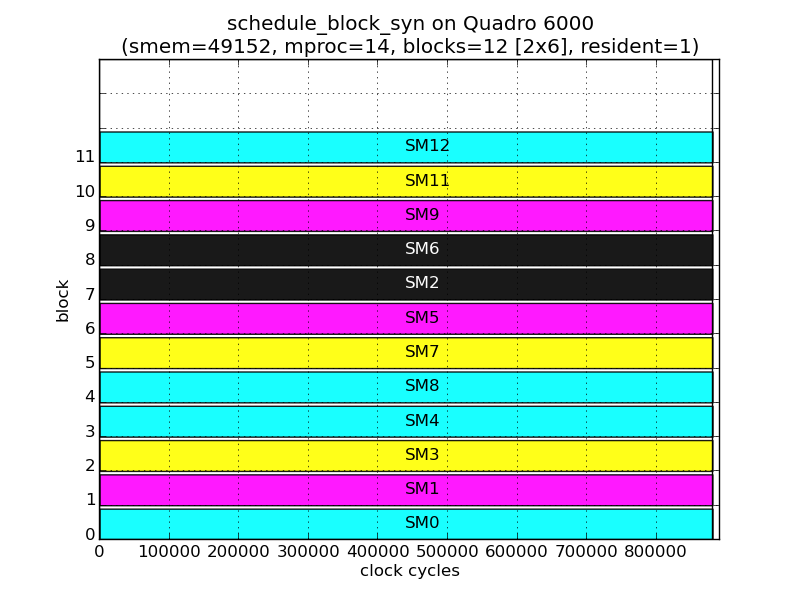
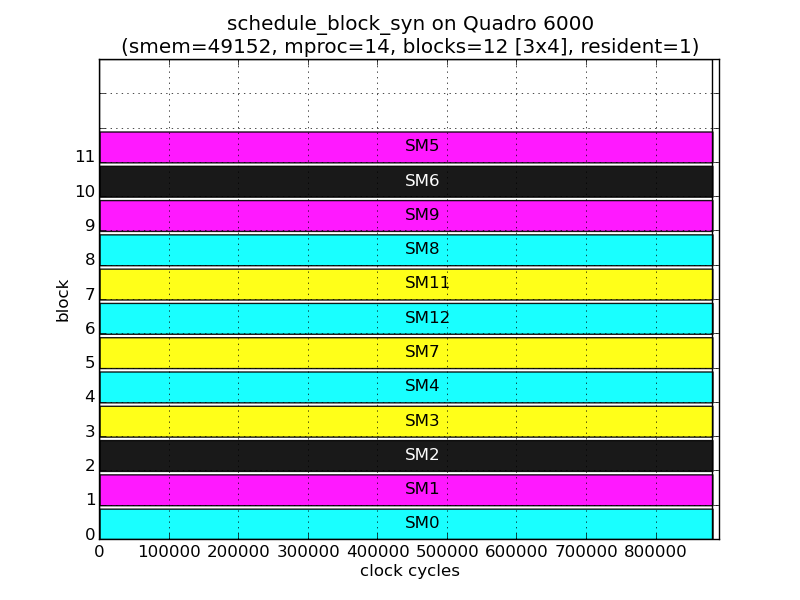
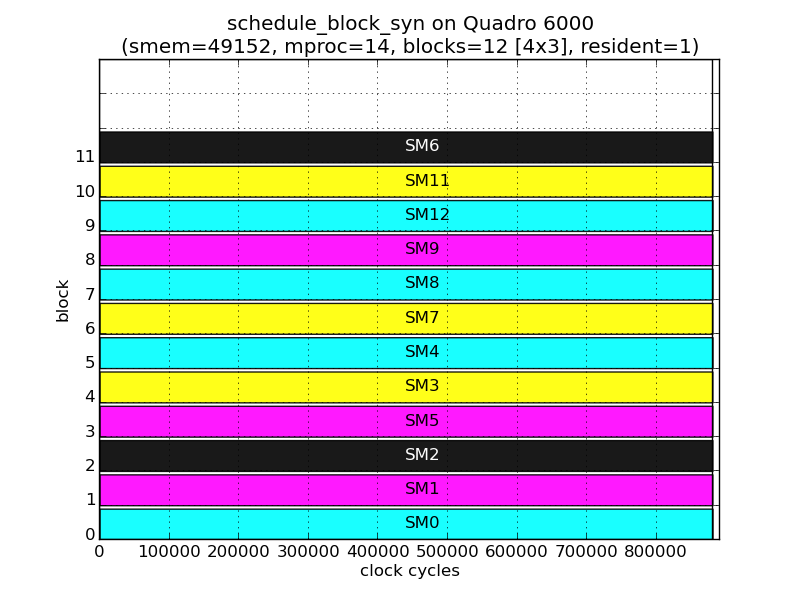
Although the number of thread block and residency remains the same, the thread blocks are assigned to different SMs in each grid. For example, for TB11:
| Shape | 12x1 | 2x6 | 3x4 | 4x3 | 6x2 |
| SM | 9 | 12 | 5 | 6 | 12 |
Since pick_sm() only depends on number of thread blocks and residency, we surmise that the order in which thread blocks are being scheduled changes according to shape.
The following tables show the assignment of SMs to each thread block in the grid.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 4 | 1 | 2 | 7 | 8 | 5 | 6 | 11 | 12 | 9 |
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 3 | 4 |
| 2 | 8 | 7 |
| 3 | 5 | 2 |
| 4 | 6 | 9 |
| 5 | 11 | 12 |
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0 | 1 | 2 |
| 1 | 3 | 4 | 7 |
| 2 | 12 | 11 | 8 |
| 3 | 9 | 6 | 5 |
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 5 |
| 1 | 3 | 4 | 7 | 8 |
| 2 | 9 | 12 | 11 | 6 |
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 5 | 6 | 9 |
| 1 | 3 | 4 | 7 | 8 | 11 | 12 |
Let's assume that the SMs were picked in the same order as the 1-D case. We can then replace the SM IDs in the cells of the 2-D tables above with the order (equal to block ID) from the 1-D case:
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 3 |
| 1 | 1 | 2 |
| 2 | 6 | 5 |
| 3 | 7 | 4 |
| 4 | 8 | 11 |
| 5 | 9 | 10 |
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0 | 3 | 4 |
| 1 | 1 | 2 | 5 |
| 2 | 10 | 9 | 6 |
| 3 | 11 | 8 | 7 |
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 0 | 3 | 4 | 7 |
| 1 | 1 | 2 | 5 | 6 |
| 2 | 11 | 10 | 9 | 8 |
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 4 | 7 | 8 | 11 |
| 1 | 1 | 2 | 5 | 6 | 9 | 10 |
Clear patterns now emerge, all of which can be seen in the scheduling of 5x5 (residency 2) grid below which continues to show order of scheduling instead of SM.
So for 2-D grids, pick_blocks chooses thread blocks along a curve that closely resembles space-filling curves. However, it is simpler, only scanning thread blocks along primitive ⊔ and ⊓ paths in each multirow containing two rows of the original grid. Even-numbered multirows are scanned by ⊔ from left-to-right, while odd-numbered multirows are scanned by ⊓ from right-to-left. Each ⊔ and ⊓ contains 4 thread blocks. For grids with an odd number of columns, the last column contributes only vertical segments each containing 4 thread blocks. For grids with an odd number of rows, the last row is swept horizontally in the opposite direction of the preceding multirow.
It should now be clear why blocks 8 (2, 0) and 12 (3, 0) ended up waiting in the initial example of the 4x4 grid:
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 0 | 3 | 4 | 7 |
| 1 | 1 | 2 | 5 | 6 |
| 2 | - | 13 | 10 | 9 |
| 3 | - | 12 | 11 | 8 |
4.3 Implementation
A full implementation of the above algorithms in Python is available. Also included is the synthetic kernel used to probe the TBS. Finally, a verifier compares the generated schedule against an actually recorded schedule.
4.4 Cases not Covered
The scheduling of 3-D grids has not been checked.
It is not yet known if the `pick_sm()` is used for a newly arrived kernel if another independent kernel is already running (i.e. a concurrent kernel).
The Kepler succeeded the Fermi, but I haven't looked at it yet.
5 Recommendations
If you're using small, static grid sizes in your code, make sure that all thread blocks in that grid will perform work, since that's what the TBS assumes. If not, your code will exhibit load imbalance that is further exacerbated by the TBS, as observed by Liu et al. and Samadi et al.
If your algorithm can benefit from 2-D locality, it might make sense to use a 2-D grid if you're not already using one.
6 Conclusion
The Fermi TBS strives to achieve load-balance across GPCs for all grid sizes using a prioritized round-robin algorithm. Further, for 2-D grids, it picks blocks in a pattern resembling well-known space-filling curves, perhaps to preserve 2-D locality.
7 Appendix
7.1 Mapping SMs to GPCs
SMs on the Fermi are organized into Graphics Processing Clusters (GPCs) which contain up to 4 SMs each. Some GPCs can contain fewer SMs. To the best of my knowledge, there is no way to directly figure out the GPC to which an SM belongs. I use an indirect way, the value of clock64(), which I presume is shared by all SMs in the GPC (as it was in pre-2.0 GPUs containing TPCs).
For this to work, the values of clock64() must be sufficiently different in each GPC to distinguish them from each other. Fortunately, the values of clock64() in each cluster are indeed distinct, at least on the GPUs to which I have access. In the figure below, all the thread blocks start together at nearly the same wall clock time. Each horizontal bar represents a thread block, with the number in the center of the recording the %smid value. Of interest to us here is the number in the beginning of each bar, which is the value of clock64() when the thread block started. Here, the value has been adjusted by subtracting the minimum clock64() across all SMs from it. That is, it is the offset from the "earliest" clock source.
The figure reveals that SMs 0, 4, 8 and 12 clearly share a clock source and presumably are part of the same GPC. The other clusters are {3, 7, 11, 13}, {1, 5, 9} and {2, 6, 10}, the last two containing only three SMs each.
It is not clear which cluster is GPC0 and so on. I assume that GPC0 contains SM0, GPC1 contains SM1, etc.
8 Postamble
I figured these algorithms out in October 2011 during my PhD when the Fermi was still relatively new. At that time I only had access to a Tesla C2070. Those older descriptions relied entirely on clock64() offsets to figure out the algorithm because I had no idea that %smid existed. Ashwin Prasad, my fellow student at that time, later told me about %smid which enabled this document written in 2014 to be much simpler. The packaged code, however, still contains some cruft reflecting the absence of %smid. Finally, recent access to the Quadro 6000 and GeForce GTX 480 helped cement and simplify the way `pick_sm()` worked, so I'm now fairly confident that the algorithms are correct.