
Array: 3 1 4 1 rows = 3, cols = 4
5 9 2 6
5 3 5 8
is stored in sequential memory locations as
3 1 4 1 5 9 2 6 5 3 5 8
^
start----|
offset 0 1 2 3 4 5 6 7 8 9 10 11
i(row) 0 0 0 0 1 1 1 1 2 2 2 2
j(col) 0 1 2 3 0 1 2 3 0 1 2 3
In a (L by M by N) 3-D FORTRAN array, where indices start at 1 and the array is stored so that the first index varies fastest, element (i,j,k) is found at offset (k-1) + N((i-1) +L(j-1)) (I think! You can check to see if this works). All that is irrelevant to this assignment... it just provides the motivation, but now you know something about (one form of) array indexing. The fact that Arr[row][col] evaluates to the contents of the correct offset OR(!!) the contents of the correct cell in the vector-of-pointers representation I showed you briefly on day 1 of class is due to the compiler recognizing the pun and interpreting the [] as input to the index calculation or the pointer incrementation and following depending on the declaration. Cute, eh?
Anyway, in either of those array storage schemes, if the array is sparse (has few elements) it is wasteful to devote the necessary storage to all the zeros:
0 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 9 0 0 0 4 0 0 0 0 6 0 0 0 3 0 0 0 0
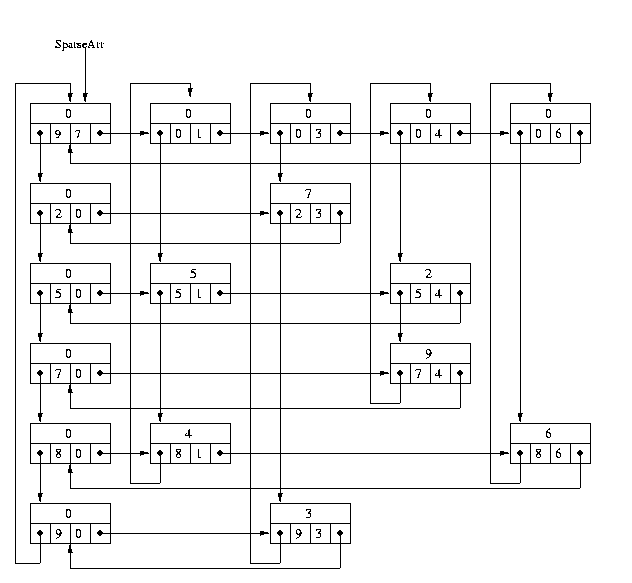
Thus one arrives at some data structure or other for a sparse array. One such data structure, made of linked circular lists, for a sparse array is shown below.

Objects and references (pointers) in a sparse array.
Each element in the SparseArray is an object of type SAElement holding a next-elt-in-row (right) pointer, a next-element-in-col (down) pointer, a row number, column number (not strictly necesssary, but think about the alternative), and the contents of that array element (usually a real number). The array header has the number of rows and cols and the row and col headers have the number of the row or column they represent in the appropriate field.
A variant on the structure shown might have doubly-linked lists, if moving both forward and backward in the row and column lists is a usual operation. Note that there are headers for each row, column, and one for the whole array, with appropriate values so you can tell what they are.
Methods on the class SparseArray are the usual ones. Let us consider the following: {construction, insertion, printing, duplication, addition, transposition .
public SparseArray() returns an object of type SparseArray.
public void Insert(int row, int col, float value) creates an object of type SAElement, fills its fields with the given row, col, and value values, and and links it into the correct row and col of arr. Note that this may be easier or harder depending on whether it has to create new header nodes for the row and col in question.
public void Print() does the obvious thing. Definitely needed for debugging, and a good test that all the pointers are in place.
public SparseArray(SparseArray arr2) does the obvious thing. Could do it with a Create and a bunch of Inserts, or could work directly from one object to the next.
public static SparseArray Add(SparseArray arr1, SparseArray arr2) creates a new array that is the sum of the first two. Sums go elementwise. The arrays have to have the same number of rows and columns.
public SparseArray Transpose () creates and returns array from this SparseArray such that B(i,j) = A(j,i).
For fun and extra credit, you might want to implement public static SparseArray Multiply (SparseArray A, SparseArray B), which creates the matrix product of the two arrays. Your function should check that there are as many cols in A as there are rows in B, (A is (R x K) and B is (K C)) and compute
Product(i,j) = SUM from k=1 to k=K of ( A[i,k]* B[k,j]).
Thus you should consider a SparseArray sparse array class with member functions to do the above sorts of manipulations, a constructor to do the creation, a destructor to clean up the storage, etc., all in good, well commented, JAVA style.
Your main() method should be an interactive command loop (a ``loop forever'' reading keystrokes that are used to select clauses of a switch statement that do the indicated operations.) You could have an array of pointers to sparse arrays, and refer to them by index in your commands, thus:
ckipdat? // this is the prompt ckipdat? c 0 //ie. create an array in the 0th element of array what size? 3 4 ckipdat? p 0 0 0 0 0 0 0 0 0 0 0 0 0 ckipdat? i 0 indices, value? 0 2 7 ckipdat? p 0 0 0 7 0 0 0 0 0 0 0 0 0 ckipdat? t 0 ckipdat? p 0 0 0 0 0 0 0 7 0 0 0 0 0 ckipdat? c 1 //ie. create an array in the 0th element of array what size? 4 3 ckipdat? i 1 indices, value? 1 1 9 ckipdat? p 1 0 0 0 0 9 0 0 0 0 0 0 0 ckipdat? a 0 1 2 // add arrays in 0 and 1, put sum in 2 ckipdat? p 2 0 0 0 0 9 0 7 0 0 0 0 0 ...
Thus you can interactively create and operate on matrices and print them out. You should save one of these interactive sessions, illustrating all the capabilities of your program. Include the script in your Readme file. See the web page for what else is expected in the Readme file, how to use the Turn-in script, etc. Don't forget proper formatting, helpful identifiers, and helpful comments.
This page is maintained by Chris Brown
Last update: 5.18.99., T. F. Pawlicki