Circuits

LOGIC and CIRCUIT DESIGN

From Found. of C.S., Aho and Ullman Ch. 13 (Reserve) and On Line.

• High and Low voltage levels encode true and false (1 and 0).
• Circuit design shares many principles with algorithm design -- modularity, divide and conquer methods.
• Circuits are often parallel: simpler ``data model'' than a programming language.
• Costs: Number of gates (surface area), depth, fan-in, fan-out, (packaging).

CONCEPTS

Gates (primitive circuits for logic operations)

• Gates organized into circuits.
• Combinatorial circuits: equivalent to logical expressions.
• Karnaugh Maps for minimizing circuit size: charming "Victorian" graphic technique: can't imagine it's practical nowadays but it's instructive.
• Practicalities like physics and timing properties.
• Adders: ripple-carry and divide-and-conquer.
• Circuits with memory (unlike combinatorial ones).

GATES

Each one does a Boolean function:

AND, OR, NOT, NOT-AND (NAND), NOT-OR (NOR).

Number of Boolean Functions on n inputs: 2^{2^n}, from boring (e.g. constant) to universal (e.g. NAND, NOR). A B AND NAND OR NOR 0 0 0 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 1 0 1 0 In the literature we write + for OR, use 'multiplication' for AND, and the macron (overbar) for NOT. In HTML there's no way to put any accents over most letters, so I'm stuck with using x' for NOT(x).
e.g.: x + ( x'y' )+ (yz).

Build other functions out of gates:
x ⇒ y is x' + y.

GATE SYMBOLS

CIRCUITS

Combinatorial (gate's output cannot reach its input -- no cycles in gate-connection graph.)

Opposite is Sequential, which correspond directly (in a formal, provable sense) to deterministic finite automata. The circuit's output is 1 for an input if and only if automaton accepts corresponding input.

E.g. of combinatorial circuit to compute
Z = X ≡ Y

SEQUENTIAL CIRCUIT EXAMPLE

LOGIC TO CIRCUIT

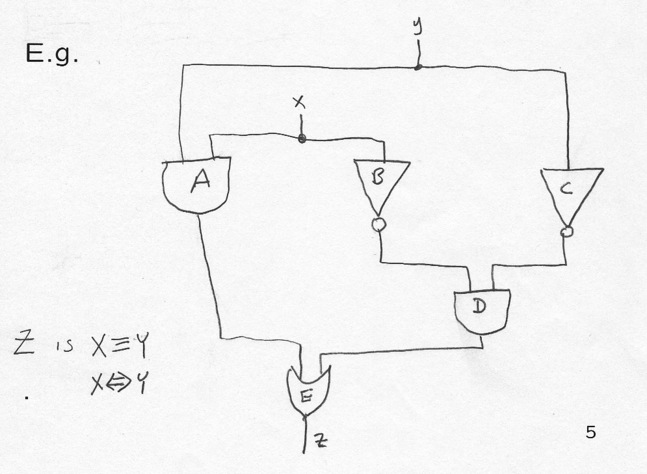
Given Logic expression: using Structural Induction (very FOCSy!): Circuit will be a tree (as expected). Consider the expression as a tree (say fully parenthesized).

Basis: if expression tree is a single node, the expression can only be an input, say x, and the circuit is this input itself.

Induction Otherwise the expression has a logical operator θ at the root and has a number of subtrees E_i for θ's arguments.

LOGIC TO CIRCUIT CONTINUED

Our inductive hypothesis applies to the subexpressions (subtrees), so there is a circuit C_i for each E_i. To build the circuit, take a gate for operator θ and give it n inputs, one from each of the C_i in order, and the output for this new circuit is the output of the θ-gate.

Note this is a super-literal approach to circuit design that doesn't notice shared subexpressions or other simplifying transformations.

CIRCUIT TO LOGIC

Know circuit must be a tree, so we can pick a topological order of its nodes (gates) such that if the output of the ith gate in the order feeds an input of the jth gate in the order, then i < j. (see Topological Sort, a three-line algorithm that uses DFS and inserts nodes into a list sorted by depth -- first textbook example of an important DFS algorithm). A topological sort is an ordering of vertices in a directed acyclic graph, such that if there is a path from u to v, then v appears after u in the ordering. No cycles; start with vertex with no incoming edges; output it, remove it and its edges, repeat.

Two of many Topological Orders: A B C D E, C B D A E

CIRCUIT TO LOGIC CONTINUED

Induction again, this time on variable i in the statement S(i): For the first i gates in the topological order, there are logical expressions for the output of these gates.

Basis: at i=0, nothing to prove, done.

Induction: for ith gate in order, say inputs are I₁, ..., I_k. If I_j is a circuit input, say x, then let the expression E_j for input I_j be x. If I_j is output of some other gate, that gate must precede i in the order, so its expression has already been constructed. Let operator associated with gate i be θ.

Then expression for gate i is θ(E₁, ..., E_k), or for strictly binary operators could write (E₁) θ (E₂).

ONE-BIT ADDER: Continuing Exampls

KARNAUGH MAPS 1

Sum of Products Expressions (Disjunctive normal form) From truth-table to minterms, sum (OR) of which is what we want.

One-bit adder TT x y c d z d minterms (1 if each var matches row values) 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 x'yc 1 0 0 0 1 1 0 1 1 0 xy'c 1 1 0 1 0 xyc' 1 1 1 1 1 xyc Take sum (OR) of minterms of rows with value 1. This expression is 1 when inputs match one of rows for which function is 1. x'yc + xy'c + xyc' + xyc. That's the DNF for the boolean function d.

KARNAUGH MAPS 2

KMs find sum-of-product expressions for Boolean functions, tend to be simple (efficient) solutions.

KM is n dimensional tabular form for n-argument Boolean function: practical up to n=4.

Note if we have two minterms differing by one variable's negation, can forget (delete, pitch) that variable! (pq + p'q) ≡ q. This is the idea behind creating bigger implicants.

q(p+p') ≡ q(TRUE) ≡ q .

IMPLICANTS

An implicant for Boolean function f is a product x of literals for which no assignment of values to the variables of f makes x true and f false. Thus, by prop logic (!) if the implicant is true the function is true. For example, every minterm for which the function f has value 1 is an implicant of f.

An implicant covers the points for which it has value 1. So a logical expression for a Boolean function could be the OR of a set of implicants that together cover all points where function value is 1. A prime implicant for f is one with as few literals as possible: it ceases to be an implicant for f if any literal is deleted. That is, if we double its size it will cover a point with value 0.

2-D KARNAUGH MAP E.G.

2-D KARNAUGH MAPS

A rectangle corresponding to an implicant can either be a single point, (corresponding to a minterm). OR a row or column (corresponding to pair of points that agree in one variable and disagree in the other). This reduces to the single variable they both share. OR the entire map, in which case the product reduces to the constant 1, and function is TRUE, which has 1's at every point.

The bigger the rectangle, the fewer literals in the product. We generally like fewer literals, which means fewer operators, which means simpler. So we might want to consider only prime implicants to cover a map.

WHY KARNAUGH MAPS? 1

WHY KARNAUGH MAPS? 2

3-D KARNAUGH MAPS 1

Map the cube onto 2-D in such a way that adjacent columns correspond to assignments of truth values that differ in only one variable. Also columns ``wrap around.'' The carry-out function looks like

3-D KARNAUGH MAPS 2

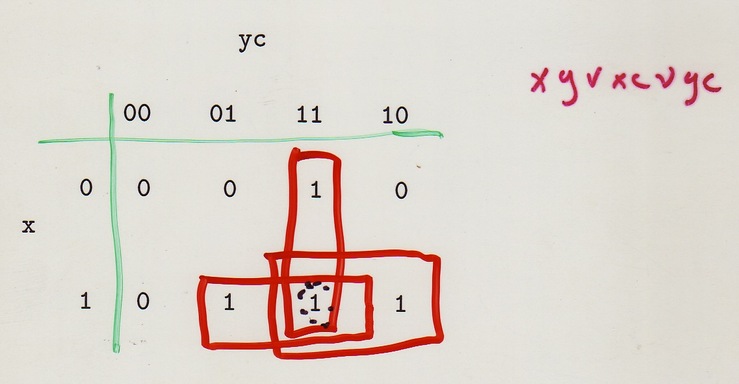
Which rectangles can represent implicants? Must be product of literals. In a product, variable appears negated, not negated, or not at all. When it appears (negated or not) it cuts in half the number of points in corresponding implicant So number of points always a power of 2.

Each permissible implicant is collection of points that, for each variable, either includes only points with that variable equal to 0, or includes only points with that variable equal to 1, or does not discriminate on the basis of that variable.

So in 3-D we get 1) any point; 2) any column; 3) any pair of horizontally adjacent points, including wrap-arounds in cols 1,4; 4) any row; 5) any 2 x 2 square of 2 adjacent cols, including wrap-arounds; 6) the entire map.

PRIME IMPLICANTS 1

Prime implicants are really the point of the Karnaugh Map: they are the shortest way to represent a chunk of the truth table.

PRIME IMPLICANTS 2

PRIME IMPLICANTS 3

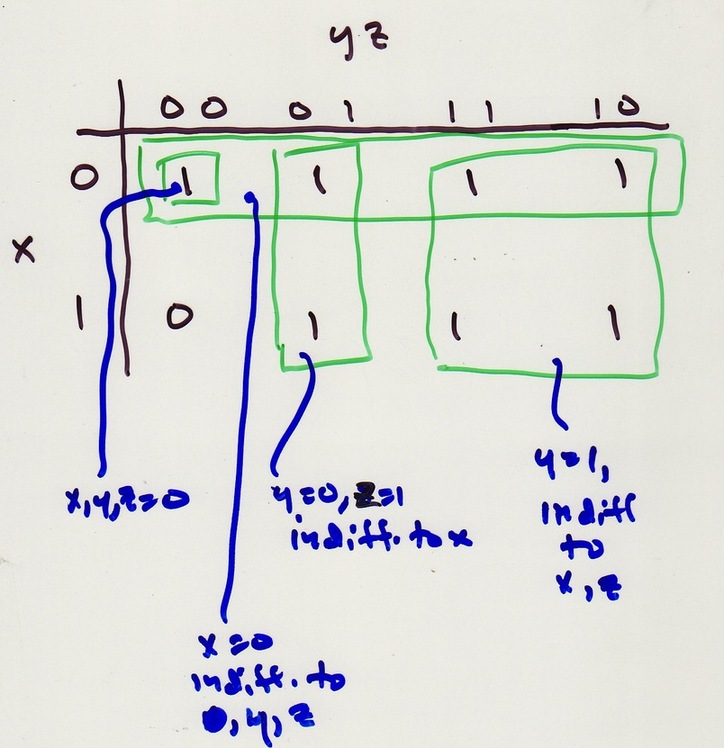
Below also a 4-D Karnaugh Map.

4-D KARNAUGH MAPS

Do the 2-variable trick on rows as well. Use same row order for pairs as col. order in 3-D for same reason. Define both row and col. adjacency with wrap-arounds. NOTE implication: 4 corner points are a 2 x 2 rectangle!

Rectangles corresp. to products of literals: 1) Any point; 2) Any two horiz. or vert. adj. points, including wrap-arounds; 3) any row; 4) any column; 5) any 2x2 square including wrap-arounds; 6) any 2 x 4 or 4 x 2 rectangle, including wrap-arounds (like first and last cols); 7) entire map.

LOGIC FROM KARNAUGH MAP

To get the product of literals that is TRUE for just the points in an implicant rectangle, let p be any variable.

1. If every point in rectangle has p = 1, p is a literal in product.
2. a If every point in rectangle has p = 0, p' is a literal in product.
3. Otherwise, some points have p=0 and some p=1, and the product does not contain a literal with variable p.

LOGIC FROM KARNAUGH MAP: EG

ONE BIT ADDER

Multiple inputs and outputs. Inputs x and y: two bits at some pos. in binary number, and c, the carry-in bit from position to right. Output: sum bit z (1 if an odd number of x,y,c are 1) and the carry-out bit d (1 if two or more of x,y,c are 1). x y c d z d 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 yc 1 0 0 0 1 1 0 1 1 0 xc 1 1 0 1 0 xy ⇒ yc ∨ xy ∨ xc 1 1 1 1 1 xyc

ONE BIT ADDER -- KARNAUGH MAP

ONE BIT ADDER -- CIRCUIT FROM LOGIC

Turns out this is a really bad and brainless idea, but it is clearly possible.

Just implement the truth-table for the one-bit adder: expect both z and d to be the ORs of ANDs and you'd expect to have to deal with seven or eight cases, one per row of the table.

Create the NOT versions of all inputs with inverters, then create AND gates for each minterm needed in any output. Number gates 1-7 (000 not needed) and think of labels as binary for the xyc inputs, 0 for negated. OR the needed minterms together, one OR for each output.

LOGIC FROM CIRCUIT

For interest's sake, going the other way is easy.

Getting the logic from the circuit means selecting a topological order: what is natural and works is NOTs, ANDs, ORs. Clearly NOT of x is x'. The output of gate 1 by definition is x'y'c, etc. The output of the OR gate for z is thus
x'y'c + x'yc' + x y'c' + xyc

And for d:
x'yc + xy'c + xyc' + xyc,

Which you can prove is same as the KM expression (how?):
yc + xc + xy.

PHYSICAL CIRCUIT CONSTRAINTS

Gate delay and circuit speed: speed goes with the number of gates on the longest path in the circuit: analgous to program running time. Technology dictates absolute time.

Dollar cost about proportional to number of gates. Circuits on large areas need longer wires, get more propagation delay. Also imperfections are more likely with larger areas.

Large fan-in and fan-out (inputs and outputs) slow down a gate in practice.

So circuits can be optimized over several criteria.

TWO CIRCUITS FOR "OR"

DIVIDE AND CONQUER ADDER

Algorithm design techniques affect circuits, too ("basic ideas keep cropping up"...CB).

Could build an adder for integers from the one-bit, delay-3 example adder. It's not bad design (can get delay two if we do all complementing outside). This gives a ripple-carry adder. So delay of 3n for n bit integer add.

OR Design n/2-bit adder, use two of them with some glue to build adder. Easy to see how to build D and C OR circuit, no? Analysis needs recurrences, which you learn about elsewhere (maybe 172?).

BAD IDEA

The glue is a problem for the adder. This won't work:

NEXT IDEA: N-ADDER SPECS

Let the left half adder compute two answers, one each for 0 and 1 carry-in. When RH completes, know which answer to choose. In fact delay for n is 3 + 2*delay(n/2) and that means total delay is 3(1 + log n). For n=32 this is 18, not 96 for ripple-carry.

We want n inputs x_i, same for y_i inputs. Outputs are:

1. s_i, i.e. s₁,s₂,..., s_n, n-bit sum (w/o carry-out) assuming no carry into the rightmost place.
2. t_i, similar but with a carry-in.
3. carry-propagate bit p = 1 if carry-out to left, assuming carry-in from right.
4. carry-generate bit g = 1 if carry-out even if no carry-in.

Note g ⇒ p but (g,p) = (0,1) is OK: (0101 + 1010).

RECURSIVE CONSTRUCTION

If n=1, have two inputs x,y, need to compute s,t,p,g -- these are governed by the logic:

s = x y' + x'y
t = xy + x' y'
g = xy
p = x + y
(As usual, work thru cases to see these are right).

s: 0 t: 1 g: - p: 1 x x x x y y y y ----- --- ---- ----- 1 1 1- 1-

BASE CASE ONE-BIT ADDER (1-ADDER)

INDUCTION

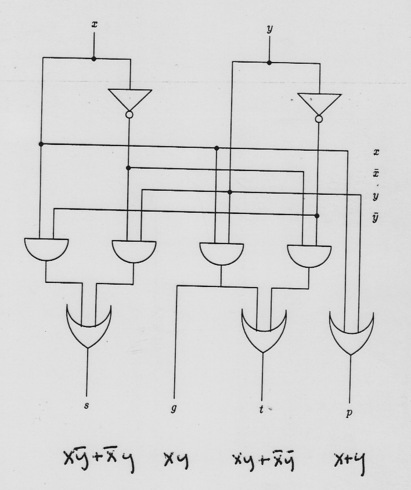
Here's our plan for the D and C adder: the FIX circuit must:

• compute the carry-propagate and generate bits for the 2n adder
• Adjust the left half of the s's and t's depending on a carry into left from right or not.

FIX IN DETAIL

If carry into R of entire 2n adder circuit. They'll be carry out at left end if either

1. Both halves propagate a carry: p^Lp^R is true: also includes R half generating carry and L half propagating. g^R ⇒ p^R, so
   (p^Lp^R + p^Lg^R) ≡ p^L p^R.
2. L half generates carry: g^L true.

Thus p for the 2n adder is p = g^L + p^Lp^R.

If no carry in on R, get carry-out at L if either

1. R half generates a carry that L propagates
2. L half generates a carry. Thus

g = g^L + p^Lg^R.

S's and T's

R half bits unchanged from output of R n-adder since L half doesn't influence it. So s_n+i = s_i^R, t_n+i = t_i^R.
See Next Diagram!

Pick a case depending on g: L half depends on how R can generate carry. If no carry in from R end of 2n adder, this is what the s_i are supposed to cover. Any carry-in must have been generated in R. Thus if g^R is true, then s_i = t_i^L, since that's the situation we pay the t's to cover. And if g^R is false, s_i = s_i^L. So
s_i = s_i^Lg'^R + t_i^Lg^R.

Pick a case depending on p: If carry-in at R half. What about t's on L? A carry into L if R propagates one (p^R = 1). So t_i takes its value from t_i^L if p^R is true, and from s_i^L if p^R is false.

FIX SUMMARY

Inside FIX we have circuits (depth at most 3, it turns out) for
p = g^L + p^Lp^R.
g = g^L + p^Lg^R.
s_i = s_i^Lg'^R + t_i^Lg^R, for all i
t_i = s_i^Lp'^R + t_i^Lp^R, for all i

E.g. for t_i:

ADDER DELAYS

D and C Adder:
Super-simple recurrence: Base-case 1-adder has delay 3, so does the FIX.
D(1) = 3
D(2n) = D(n) + 3.
So D(1) = 3, D(2) = 6, D(4) = 9, D(8) = 12...
D(n) = 3(1+ log n).

Ripple Adder:
D(n) = O(n).

D and C ADDER GATE COUNT: PICTURE

D and C ADDER GATE COUNT: MATH

G(1) = 9 by counting, then G(2n) = 2G(n) plus FIX gates. FIX can invert g^R and p^R, then needs 2 ANDs and an OR for each of the n s_i's and t_i's, and we need 2 gates each to compute g and p. So FIX needs 6n+6.

G(1) = 9
G(2n) = 2G(n) +6n + 6

This goes like 1:9, 2:30, 4: 78: 8: 186 or in general G(n) = 3n log n + 15n -6. And fewer if pick n to be nice number say 32: can simplify the right half at all levels. Note ripple-carry adder uses fewer gates (less than half as many for n=32). Also gates grow faster (by log) in D and C. But speed so much better D and C is practical choice.

MEMORY

If load= 0: a is 1, c is 0. If d is 1, b is 1, so d remains 1. But if output of d is 0, then b is 0, so output of d remains 0 while load = 0. So circuit output stays ``what it was'' as long as load stays 0.

If load=1, a, b go to 0. Output of c will be whatever in is. And also output of d will be whatever c is, which is what in is. So changing load to 1 sets output to whatever in is. Changing load back to zero lets this value circulate between b, d.

SUMMARY

• Gates and relation to Logic
• Gates combined into Circuits
• Combinatorial and Sequential Circuits
• Circuits from Logic, Logic from Circuits
• Karnaugh Maps
• Divide and Conquer for Adder (Text has MUX too).
• Circuit Practicalities, Speed and Size
• Memory