Signal Processing

figure out format of submission! cb 4 may 2011

Introduction

This is a grab-bag of projects: Please do at least two.

Your goal is primarily the written report of your work. The expectation is that you'll be using various sources for your investigations, so make sure you cite all references you used: the more (that you actually use) the better. Technique, results, and presentation (especially graphics) are all important. The elegance and organization (and correctness) of the code count, but not as much as the report, which should contain enough information to convince the reader that your code must be correct.

Project 1: Sunspots

The SIDC has lots of sunspot activity data, I got some and put it in the Data folder for you to download. ssdata.mat is a file of monthly sunspot activity data going back to 1759, with the associated guide ssdatareadme.txt. Go read up on sunspot activity cycles, report on what you find, and see if you can verify or falsify claims from the literature by analyzing this data. If you want to look at daily or yearly data, SDIC has that too.

Project 2: Lorenz Attractor

You've seem the Lorenz attractor in Intro. DE Paper . Read more about Lorenz Attractors and Strange Attractors in the usual places (Wikipedia, Google). Try Strange Attractors.

Use your Lorenz attractor implementation from the ODE topic, or go ahead and implement it (it's a 4-line program with a 4-line ubroutine). The output is four arrays, T, X, Y, Z, where we think of a point following a path in 3-space: at time t it is at X(t), Y(t), Z(t). Plotting two of these against each other (as in plot(X,Z) ) gives the familiar "Lorenz Butterfly Diagrams".

Instead, consider the function, X(t), Y(t), Z(t). They must exhibit some periodicity to give those spirals we see in the diagram. As usual, see what you can find in the literature, if anything, on the subject. Then produce some data and analyze its frequency content. Things you can vary are: the axis (X,Y,Z) you plot and the parameters of the Lorenz DE.

Practical Introduction to Sound

Matlab has commands sound and soundsc, but I only used wavplay, wavrecord, wavread, and wavwrite. See getsound.m, putsound.m in code directory. The arrays wind up as doubles I think, but certainly as floating point numbers, and nicely enough any array of floats varying between -1 and 1 can be wavwritten as a wav file: so we can create our own sounds like pure sine, square, sawtooth waves easily.

For no good reason I used stereo wav arrays (2-columns) for time-domain work (Project 4) and mono for the frequency domain (Project 5) and the Spectrogram (Project 3).

wavread has many options, including getting meta-information (sampling rate etc) and reading big files in manageable sequential chunks. Our Data File has at least one ".wav" file in it, but there are heaps of them of all sorts out on the web, or you can make your own with a microphone, CD player, iPod, whatver.

The Simpson's theme in the data directory, and indeed most if not all of the ".wav" files on the web are actually .mp3 files, which wavread can't read (you'll get an error message). What you do is download the (bogus, MP3) ".wav" file, and if you're on one of the UR machines (I don't know what's standard on random Windows systems) go All Programs - Multimedia - Real - RealPlayer Converter. (Audacity won't read these mp3s it seems). Otherwise there are many converters out there: on Mac's OS-X system, Switch works. Convert the .mp3 to a real .wav file (thus uncompressing it) and Matlab should be happy with the result. Usually converting means no more than loading the file and exporting or saving as a .wav file. You should be asked for the .wav encoding parameters, especially samples per second.

Warning! CD quality is about 44 KHz. (standard Matlab setting is 44100 samples/second). The 11025 setting is listenable and standard. For my work I used 22050. Those three are considered standards. Even at the 11025 setting, the .wav file will be about ten (10) times as large as the .mp3 file (gives you respect for mp3, eh? You might look up what all went into this clever encoding). So you probably don't want to deal with more than a few seconds of .wav sound at a time.

Project 3: Spectrograms

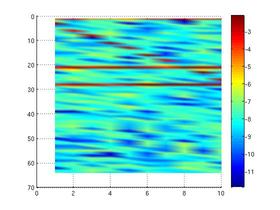
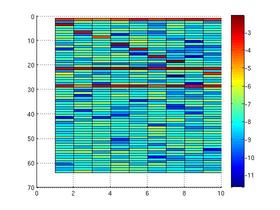
Above left (from Wikipedia) is a spectrogram of Male voice saying "19th century": vertical strips are pseudo-colored power spectra (color guide at right of image), time goes left to right. Middle and right is CB's version, showing the spectrogram of two constant-frequency sine waves and one that increases in frequency with additive uniform zero-mean noise. Here, frequency reads down, time goes left to right. There are 10 vertical strips. Matlab shading is interp in the middle and faceted (default) on right.

Read Wikipedia on 'sonogram' and 'short term fourier transform'. Write a spectrogram program you can use to display speech or music waveforms Just Like Downtown (as above).

If you're interested in language, maybe read about 'formants', collect a few samples of speech and see if you can identify the formants in your sonograms. If not, maybe analyze some of your favorite music and describe what the sonogram is showing us.

Projects 4 and 5: Guitar Effects

The Assignment

I wanted to know something about guitar effects. For these two projects I'm giving you my code , which probably has more never-do-this howlers than it has good ideas. You are invited to use it, improve it, or extend it as your interests take you. Just put in some work and tell us what you did in your report, which will be an HTML page with pointers to your sound samples. I think you can improve everything I did or you can add something new...wah-wah pedal, ring modulator, phase- shifter, effects I never heard of, whatever. I only used first-level Google and Wikipedia for how-to's. If you want to apply my code or modify it, the exercise is in understanding and using someone else's ratty code. Main thing is you have fun, process signals, and learn something.

Guitar Effects

Go to Guitar Effects Explained .

In fact, if this flakey site is misbehaving, just look up "chorus effect", "phaser effect", "flanger" "ring modulator", etc. on Wikipedia. Our goal is to understand how to implement these effects digitally, not necessarily to understand all the math (if any) or diagrams. I think it will be clear how to take some sound waveform data and implement our choices from chorus , phase-shifter , flanger , delay , ring-modulator .

All this work can be done in the time-domain just by shifting, multiplying, and adding time-signals. In this business they seem to call a small shift a "phase shift" and a big one a "delay". Fair enough, they're at different timescales.

Acknowledging my ignorance about how proprietary products work, and realizing we're stuck in a digital, not continuous, world, the section below gives my understanding. Code I wrote (no guarantees on content OR style!) are in the SP code directory.

PRACTICAL TIP. One of my basic coding principles is When Developing Code, Always Be Able To Tell If An Output Is Reasonable Or Gibberish. So there's a Corollary: Never Use Real Data Until Last Minute. These principles account for the possibly puzzling plot commands in my sound code. That's because I started off not using getsound at all -- I started off generating my own simple-minded inputs, like a single sine wave or ramp (straight line function), to see how it was affected by my effects. A delay should cause a visible shift. A swept delay should cause the output sine wave to lead and then follow the input. Etc.

Guitar Effects: Time Domain

See getsound.m, putsound.m in code directory. The arrays wind up as doubles I think, but certainly as floating point numbers, and nicely enough any array of floats varying between -1 and 1 can be wavwritten as a wav file: so we can create our own sounds like pure sine, square, sawtooth waves easily. For no good reason I used stereo wav arrays (2-columns) for time-domain work and mono for the frequency domain (below).

Given a wav array (Sound, say), it's easy to delay it: assume it's preceded by zeroes and so delayedSound(i) = Sound(i-Delay);. Issues arise because we usually like to think about delays in seconds (echoes) or milliseconds (for flangers, say), or somewhere in between for other effects. So we need to convert from Hz to indexes, and that depends on the sampling frequency. This motivates my various unit-changing utilities.

Can we simulate someone singing or playing sharp or flat with time-domain techniques? Not simply! We can take every other sample in a wav array and get one which, played back at the same rate, is an octave higher. BUT it's only half as long. If you want achieve the Alvin Effect , you've got to sing at half speed and THEN speed up your playback or sample down. Likewise interpolating samples twice as frequent as the original wav array gives you an octave down and twice as long.

You should understand linear interpolation, since it's basic. The code's in the directory, but the idea is just that if you have two points (x0,y0) and (x1,y1), if you approximate the function between them by a straight line, the value of an x that is p percent of the way from x0 to x1 is the "interpolated" value of y that is p percent of the way from y0 to y1.

For a chorus effect I need the voices to pretty much stay together. I do have a "constant delay" effect, which just shifts the wave in time (array index).

For my swept "Delay" effects (see the reading for concepts like Sweeping, Sweep Depth, etc.), I (sinusoidally) sweep, or increase and decrease, the resampling rate to create a distorted version. The new 'voice' alternates between being lower and slower and being higher and faster, so on the average it doesn't fall behind the original.

Thus we have a function f given by the sweep waveform and parameters that tells us in this case how 'delayed' (or 'advanced') the sample at Wnew(i) should be: what sample from Worig gets written into Wnew(i)? Usually the 'sample index' from Worig is not an integer, hence our need to interpolate Worig to get values for Wnew.

So we just work through Wnew's indices i = 1:N, computing (from a function f given by sweep waveform and parameters) a 'delayed' (could be negative) x value f(i). Interpolate f(i) into the original wav array and the result is the value at to re-sample at some x+dx.

My delay effect has several parameters: I use an exponentiated sine as a sweep function: Raising the sine to fractional powers makes for a faster rise and fall, approximating a square wave as the exponent shrinks. Positive exponents make the wave stick near 0 more, and have sharper peaks. In my experience fast changes in sweep lead to annoying discontinuities, but more experimentation is needed. As parameters, I have the amplitude (sweep depth), frequency, and phase of the sweep wave, maximum and minimum delay in milliseconds, and a final volume for the voice.

My pitch effect really does exactly the same thing but with different semantics (and implementation -- probably not necessary). Instead of microseconds the sweep is over sharp to flat pitch variations in terms of half-steps (a sampling rate of 2^1/12 = 1.0595 will raise the pitch one half step). The pitch of a sound varies with the rate of sampling, and so the effect simulates a sampler that runs faster and slower, again averaging out to zero delay.

With a single sine wave, say Concert Pitch A440, the pitch effect would not so obviously display the tempo changes (but the highest pitches still last longer than the lowest). Here's A440 , and here's the output of my pitch effect , which goes sharp and flat at the rate of 1 Hz. Now if these were evenly-sampled waves you'd expect to get some cool microtonal exercise increasing and decreasing dissonance by adding these two waves up. Instead, since they also speed up and slow down, you get a mess.

My final time-domain effect is simply 'vibrato', which for me is sinusoidally varying the amplitude of the elements in wav array, so the same sound gets periodically louder and softer.

Compare this Solo and the baritone quintet version. There's one pure delay (25ms), one swept delay (30-50 ms), one swept pitch variation ( ± a semitone), one vibrato (20% at 10hz) and a cascaded pitch variation + vibrato voice. All those voices sort of blur together and average out... could be more dramatic as a carefully selected trio.

Now flanging turns out to be exactly the same thing as swept delay except the delay is around 1-10 ms, and often flangers have several stages (operate on the input sequentially, with stages feeding into one another or back to themselves). Here is my version of a rhythm section , a flanged version with a sweep depth from .1 to .4 ms, then that fed back (in series) 3 times , and 2 flangers in series (The previous and one with sweep from 2 to 10 ms.

Project 5: Pitch Adjustment

To do the chorus effect, you need to vary pitch a little. How would you raise all the pitches in a sound file up a half-step? If all the frequencies were multiplied by two (the frequency component for 200 Hz in the input is moved to 400 Hz in the output, etc.), the whole voice or orchestration or generally sound would go up an octave (12 half-tones). So to shift up a half-step we need to multiply all the frequencies by the twelth root of 2, or 2 ^1/12.

Now there's a problem. Imagine the power spectrum PS of our original sound wave, displayed in "fftshift" form, symmetrical around the center: Imagine it's indexed from -N:N. If we move the power values to a new array HighPS where they have twice the frequency, then PS(1) goes to HighPS(2), 2 goes to 4, N/2 goes to N, and N/2 through N go nowhere! We've lost 1/2 the values defining what the original wave was. There may be less energy up there but high frequencies are definitely important for sounds like ssssibilants and ffffricatives, anyway. oops.

Below, I broke the wav array (created by sampling at 22050 samples/sec) into 8192 -long segments (this is the time domain, remember)... so that would be 8192/22050 = .3715 second-long segments, pitch-shifted each, and pasted the results together again. (It's the same code that created the sonogram above, by the way), only computing and displaying the power specta after the temporal break-up).

Here is a Solo , a frequency-domain synthesized fifth above , and a duet , with the melody and major third above.

There are professional items like real-time guitar effects, pitch correction apps for iPhone, and voice transformatioqn. I couldn't find much about pitch correction products on line, but check this out to see how careful you need to be to work with human voices: Voice Transform Site , and take a look at the papers pointed to early on by Kain & Macon and Yegnaranayana et al.

Project 6: Image Reconstruction

Impress us with some image reconstruction.

Our Data File has three .jpg images of license plates but they may be getting a bit stale. Grab an image from the web, blur it with some 2-D PSFs and try to recover the original. Good candidates are the disk (out-of-focus blur), gaussian (very nice numerical properties), and a 2-D path like the following, presumably represented by an array of 0's and 1's.

For all these cases, you know the PSF exactly and mathematically everything should work wonderfully. Does it, and if not why not?

Try to do reconstruction on an image you make. You could set up some small light source and make a motion-blurred image: the image of the small source shoud be your PSF. Then go in and extract the PSF and do the deconvolution.

Or shoot a picture of a scene through a chainlink fence, venetian blind, window screen. Then shoot the same picture with a white (say) background set up behind the fence, blind, or screen. Now you are in a position to make a filter that should remove the f,b,or s effect from your photo of the scene. Does it work, and if not what happens?

What to Hand In

See the Universal Hand-In Guide.

Briefly, for the Code component of this assignment, you'll need a .zip (not .rar) archive with code files and README.

Submit the writeup as a single, non-zipped .PDF file.

Submit before the drop-dead date for any credit and before the due date for partial-to-full (or extra!) credit.

Check immediately to see BB got what you sent!