Welcome to CSC 282/482 (02.24.2022)
Minimum Spanning Trees
- General algorithmic solution
- Kruskal's Algorithm
- Prim's Algorithm
Minimum Spanning Trees
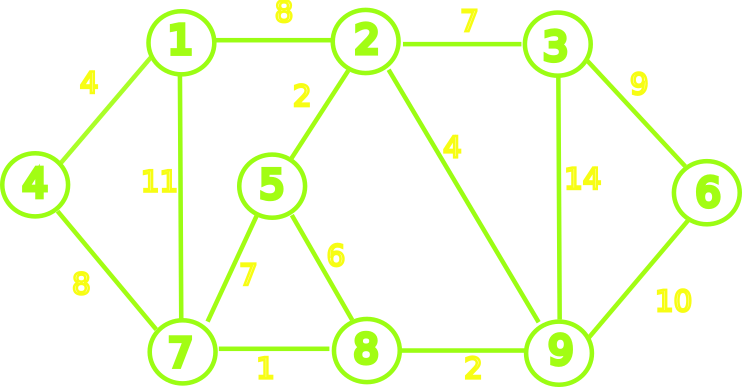
Given an undirected weighted $G=(V,E)$. We want to find $T \subseteq E$, acyclic and connecting all vertices.
- We call $T$ a spanning tree
In addition, we would like to minimize the weight of $T$ given by: \begin{array}{c} w(T) = \sum_{(u,v) \in T}{w(u,v)} \end{array}
- The tree $T_{min}$ with the minimum possible weight is called a minimum spanning tree for $G$.
Minimum Spanning Trees
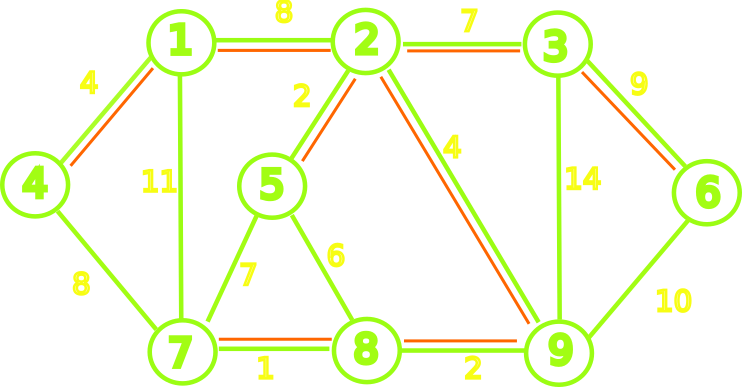
Given an undirected weighted $G=(V,E)$. We want to find $T \subseteq E$, acyclic and connecting all vertices.
- We call $T$ a spanning tree
In addition, we would like to minimize the weight of $T$ given by: \begin{array}{c} w(T) = \sum_{(u,v) \in T}{w(u,v)} \end{array}
- The tree $T_{min}$ with the minimum possible weight is called a minimum spanning tree for $G$.
Minimum Spanning Tree
Notation and definitions
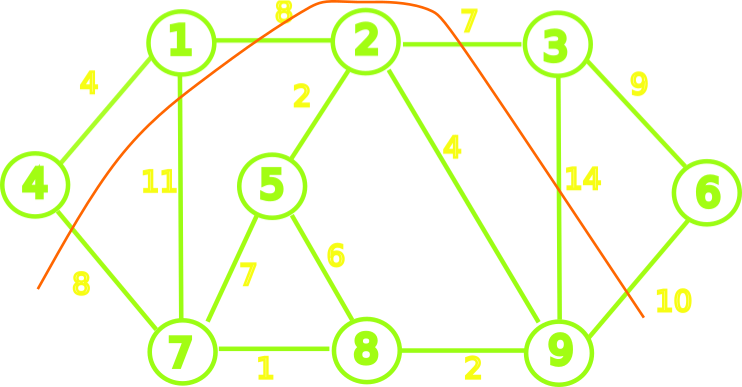
- A cut $(S, V-S)$ in an undirected graph $G = (V, E)$ is a partition of $V$.
- An edge $(u, v) \in E$ crosses the cut $(S, V-S)$ if one of its endpoints is in $S$ and the other is in $V-S$.
- A cut respects $A \subseteq E$ if no edge in $A$ crosses the cut.
- an edge is a light edge crossing a cut if its weight is the minimum of any edge crossing the cut.

Minimum Spanning Tree
Notation and definitions
- A cut $(S, V-S)$ in an undirected graph $G = (V, E)$ is a partition of $V$.
- An edge $(u, v) \in E$ crosses the cut $(S, V-S)$ if one of its endpoints is in $S$ and the other is in $V-S$.
- A cut respects $A \subseteq E$ if no edge in $A$ crosses the cut.
- an edge is a light edge crossing a cut if its weight is the minimum of any edge crossing the cut.
Minimum Spanning Tree
Theorem Let $G = (V, E)$ be a connected, undirected graph with a real-valued weight function $w$ defined on $E$.
- Let $A$ be a subset of $E$ that is included in some $MST$ for $G$
- Let $(S, V-S)$ be any cut of $G$ that respects $A$
- Let $(u, v)$ be a light edge crossing $(S, V-S)$.
Claim: Edge $(u, v)$ is safe for $A$.
Corollary: $C = (V_C, E_C)$ be a connected component (tree) in the
forest $G_A=(V, A)$.
Let $(u, v)$ be a light edge connecting $C$ to some other component in $G_A$.
Claim: Then, edge $(u, v)$ is safe for $A$.
Minimum Spanning Tree
Corollary: In addition to the assumptions of the theorem, let
- $C = (V_C, E_C)$ be a connected component (tree) in the forest $G_A=(V, A)$.
- $(u, v)$ be a light edge connecting $C$ to some other component in $G_A$.
Claim: Edge $(u, v)$ is safe for $A$.
Minimum Spanning Tree (Kruskal 1956)
The first algorithm maintains a forest of components and it reduces the number one at a time. In pseudocode: \begin{equation*} %\setlength\arraycolsep{1.5pt} \begin{array}{l} KRUSKAL(G,w) \\ 1 \quad Init~F~as~empty\\ 2 \quad foreach~v\in V \\ 3 \quad\quad create~singleton~with~v \\ 4 \quad sort~edges~E~by~weight \quad \quad //~ \text{ need to select the fittest} \\ 5 \quad foreach~(u,v) \in E \quad // ~ \text{taken in order} \\ 6 \quad \quad if~u~and~v~not~in~same~set \\ 7 \quad \quad \quad merge(u,v) \quad // ~ \text{now in the same set} \\ 8 \quad \quad \quad augment~F~with~(u,v) \\ \end{array} \end{equation*}
Kruskal's Algorithm - Activity (14)


Minimum Spanning Tree (Jarnik '29/Prim '57)
The second algorithm maintains a single tree and adds an edge at a time. In pseudocode: \begin{equation*} %\setlength\arraycolsep{1.5pt} \begin{array}{l} PRIM(G,w,r) \\ 1 \quad foreach~v\in V \\ 2 \quad\quad v.key=\infty \\ 3 \quad\quad v.p=NULL \\ 4 \quad r.key = 0 \\ 5 \quad\text{populate the queue with all vertices} \\ 6 \quad \text{while queue not empty} \\ 7 \quad \quad extract~min~u \\ 8 \quad \quad foreach~v \in Adj[u] \\ 9 \quad \quad \quad if~v~in~queue~and~w(u,v) < v.key \\ 10 \quad \quad \quad \quad v.p=u \\ 11 \quad \quad \quad \quad v.key=w(u,v) \\ \end{array} \end{equation*}
Prim's Algorithm - Activity (15)
\begin{equation*} %\setlength\arraycolsep{1.5pt} \begin{array}{l} PRIM(G,w,r) \\ 1 \quad foreach~v\in V \\ 2 \quad\quad v.key=\infty \\ 3 \quad\quad v.p=NULL \\ 4 \quad r.key = 0 \\ 5 \quad\text{populate the queue with all vertices} \\ 6 \quad \text{while queue not empty} \\ 7 \quad \quad extract~min~u \\ 8 \quad \quad foreach~v \in Adj[u] \\ 9 \quad \quad \quad if~v~in~queue~and~w(u,v) < v.key \\ 10 \quad \quad \quad \quad v.p=u \\ 11 \quad \quad \quad \quad v.key=w(u,v) \\ \end{array} \end{equation*}

Thank you for the attention
References:
- [CLRS] - Chapter 23
- Dexter Kozen - The design and Analysis of Algorithms
- [Erickson] - Minimum Spanning Trees
- Borůvka, Otakar "O jistém problému minimálním" (1926)
- Robert Tarjan - Data Structures and Network Algorithms (1983)
Thank you!
