Workshops, Labs, Tutors

Scheduling: No workshops or labs in first week. Workshop TAs will organize a poll for Workshop times.

Lab reports are graded (see grading info from main page), WS has participation points (5% of course total points). And there are WS quizzes in class, maybe extra Success Facilitation Surveys too.

It's not about grades, of course... they are a side-effect.

Workshop times and places will be made up an announced soon.

Tutoring: Computer Science Undergraduate Council offers 2-6 hours of FREE tutoring, every day M-F, in Hylan 301. It will be an informal setting where you can arrive at any time and ask your nagging questions about CSC 171, 172, and a combination of other introductory and core computer science classes.

The schedule can be found here: CS Tutoring Schedule.

In 2014, Hassler Thurston (jthurst3@u.rochester.edu) is the president and a good point of contact.

Basics

172 Goals

General Advice

Your Enemies

Your Advantages

Big Oh Intro

Question: How does computation time grow as input size grows to infinity? The Order (O) expresses (an upper bound on) that growth rate. For this lecture we take O to mean "rate" not "bound on rate"

Technology? Pfui!: faster computers make operations faster, but it turns out that doesn't change the Order of a computation, which dominates all constant speedups. It's a rate of growth. E.g.s: The time to read or print a file grows linearly with file size: N times bigger, N times longer. The time to do long multiplication grows as the square of the number of digits: 

    XXX          N
    XXX          N
-----------
    XXX          N*N multiplies
  XXXX
 XXX
----------
 XXXXXX          2N output

So...?

Combining Orders: Intro

Say T1 and T2 are running times of two processes. If for input length N

T1(N) is O(f(N)) and T2(N) is O(g(N))
⇒ T1(N)+T2(N) is O max(f(N) + g(N))
= O(f(N) + g(N))

So above, O(2N) for input, O(2N) for output, O(N2) for calculations, so total time is

O(4N + N2) = O(N + N2) = O(N2).

A higher growth rate always dominates a lower: e.g.

x2 > Nx
when x > N.

Growth Plots

The intractability of high growth rates:

below, log-log plot

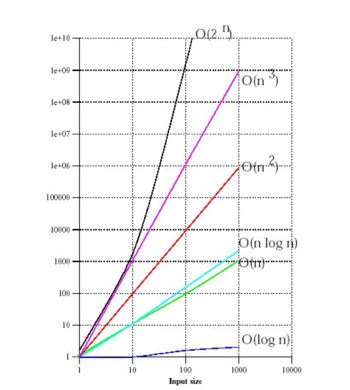
Enough: to be done right later.

Case Example: Duplicate Detection

The Problem: find identical items in a list. Practical! E.g. presenting search requests.

One solution: compare each item to all items earlier in the list. Core of the computation is: 

	for (int i = 1 ; i < a.length ; i++){
	    for (int j = i - 1 ; j >= 0  ; j--){
		if (a[i].equals(a[j])) found = true ;}}

Analysis?
Loop analysis. i counts up from 1 to length (that is N, the problem size), and for every i, we have j counting down from i-1 to zero. So...??? Answer: 1 + 2 + ... + N repetitions: sum = (N*(N+1))/2 = O(n2).

Dup. Detection: Hashing Solution

Solution: for each list item, hash(item) = is a simple O(1) function to give a repeatable, "randomized" location in a big array. Look at hashed location:
if location empty, put item there, unique (so far). O(1).
if item's there already, it's a match. O(1).
if a different item's there already, we see why hashing's so interesting....

Analysis: not obvious, goes back to Knuth and beyond. Good news is that at the price of more storage, we get linear O(N) performance (each comparison takes constant O(1) time.)

Live Demo

This
Worked
in
Rehearsal
...
Honest!

Runnable Code

Source Code and class files (run on unix-like KDE (java 1.7) , maybe not on linux's ubuntu (java 1.6). I had to fiddle to get it to work on a Mac...sigh. 


>>java CBDupSearch 1000
simpleSeach 
631 unique values 
Comps == 499500
n(n-1)/2 == 499500
Total execution time (secs): 0.027

>>java CBHash 1000
632 unique values 
Comps == 1368
Total execution time (secs): 0.0

Experimentation: O(n2) method

Sort of thing we do in projects... if you can generate date, exploit it. Output to disk, use excel or whatever to graph -- profs love it.

This plot's worth about a C -- no title, axis labels, or units.

End of Duplicate Search Example

Mathematical Background

Weiss's reviews (Ch. 1.2, 1.3) are cursory. If they're OK for you, quite a good sign. But feel free to look elsewhere. (All together: "Oh boy, I get to learn something new!").

Weiss 1.2 -- Math Review

To-the-point 5 page section.

Geometry and Proofs

On the One Hand

Equations are the boring part of mathematics. I attempt to see things in terms of geometry.
-- Stephen Hawking

On the Other...

SFS

Convince me, however you like*, that

1 + 3 + 5 + 7 + ... +(2n+1) = (n+1)2

* Sometimes we say: "Prove" (but that may sound scary).

And is the graphical solution to sum of 1--N an inductive proof?



---

Last update: 6/25/13 CB