Divide and Conquer Algorithms

Weiss Ch. 10.2.

We've already divided and conquered: quicksort, mergesort, one of the Max Subseq. Sum algorithms, tree traversals.

Template: Divide -- Solve smaller problems recursively (implies base case).
Conquer -- Solve original problem using solved sub-problems and doing some work to combine them.

We shall see some increasingly general solutions to the D&C recurrence. Applications are fun, including computational geometry, selection, and fast multiplication of integers and matrices.

D&C Runtimes

Master Theorem Stolen from Weiss Ch. 10.

Solving Recurrences Stolen from Jeffe at UIUC via Google "solving recurrences".

Jeffe revisits all we've seen, and adds Recursion Trees, a powerful general method that extends to "really weird" recurrences.

Recursion Trees

Bottom line: Recursion tree has a node for every reursive call (recursion and base cases). Thus T(n) is just the sum of all the time-values stored in each node of the recursion tree.

Often this sum has geometric series or geom. series-like subexpressions. Hence the special cases enshrined in the Master Theorem! More generally, one has to use 'mathematical maturity' (ingenuity, experience, intuition, perseverence, knowledge) to solve the sums. Luckily, the Big-Oh simplifications (e.g. multiplicative factors don't matter, descending geometric series dominated by first element, etc.) help a lot.

Outrageous Example. Consider in- (or pre- or post-) order traversal of (say printing) an arbitrary binary tree of N nodes. I guess the in-order recurrence would be something like:

T(1) = 1
T(N) = T(L) + 1 +  T((N-1) - L)

Where L is the size of the tree's left subtree and can vary in an unknown way from 0 to N-1. And the next recursion-level's possible values of L are going to depend on the previous one's(!). So this formulation sucks.

But it is a first-class, basic, recursive divide and conquer problem, so maybe we don't need no stinkin' recurrence equation.

So why not just draw an example ("WLOG") binary tree, note that it is the recursion tree: always 1 unit of work per leaf, and ultimately all N leaves are done in some order: *boom*. Just what you'd argue anyway, but now we appealing to a respectable, named method to make our point...devastating, eh?

Recursion Trees

Computational Geometry: Closest Points

Computational Geometry is a fun and fascinating area. Not so much any more, but there used to be academics who claimed it as their main area of expertise. You get to be visual and ingenious at the same time.

Problems like finding the convex hull, line segment intersection, triangulation and Voronoi diagrams, mesh generation (vastly important for CAD and finite-element studies), ray-tracing (graphics rendering), point-in-polygon 2-D, static, n-D, dynamic,...

Weiss: find two closest (Euclidean distance) points in a list of (x,y) points in plane.

.

Methods: There are N(N-1)/2 pairs, so in O(N²) can compute all distances with 2 for loops.
Instead, sort points by the x coordinate in O(N log N), draw an imaginary boundary dividing the set into left and right halves, or two problems half as big. At any stage, can compute d_L and d_R, the minimum separation in left and right sides, recursively.

To gain the goal O(N logN) advantage, need to cope with the d_C case, and check for shortest distance being between the two halves.

• let δ = min(d_L,d_R). We only care about
  d_C < δ, so only need consider a strip of points 2δ wide.
• For uniformly-distributed large point sets, note about O(√N) points in strip (analogous to one column of square array). So could brute-force search in O(N).
• Not guaranteed, so could sort by y, then look at pairs of points from top down, moving to next point if distance is > δ. This approach needs a little more analysis to prove don't examine too many points, turns out 7 is worst case (Weiss p 453).
• One more thing: we can't afford to do the sort at every level: that is an O(N log² N) algorithm. So we can do something cute with two lists sorted by x and y (Weiss 455).

O(N) Worst-case Selection

We saw the simple quicksort variation that gives quickselect (find the kth smallest element in set of elements. Like the median, say.) Tony Hoare invented both algorithms. Quickselect is faster because to select we only get one subproblem (answer's in this half) rather than two for sorting. BUT without a pivot selection method with guaranteed properties, both methods are possibly O(N²).

So 10.2.3 uses median-of-five partitioning to guarantee O(N) and describes and analyses some further improvements in reducing the number of comparisons -- a bit esoteric but not hard (p 458, Exercises).

Theoretically Fast Arithmetic

Full disclosure: fast arithmetic algorithms are rarely (if ever) practical. There is usually so much overhead and algorithmic complication that some of them have never been implemented, much less run. Computer Science isn't Engineering (thank God).

Multiply N-digit integers. Programming languages nowadays (Java, Matlab) implement this and it's a normal data structures assignment...using lists for the digits, say. Note that + and * are no longer unit-time operations, so some algorithm analyses will need tweaking.

Thinking about writing out a multiplication problem, easy to see we have to write O(N²) digits if the numbers are N digits long. Likewise the triple for loop needed to multiply two NxN matrices implies that's normally an O(N³) operation.

Integer Multiplication

Dealing with sign is easy, so assume positive N-digit operands X and Y.

This is the D&C chapter, so we have to ask "what if we broke X and Y into halves, Xl and Xr, Yl and Yr? Loosely, for k=N/2, we'd have
X = Xl*10^k + Xr, Y = Yl*10^k + Yr,
Then by middle-school algebra:
XY = XlYl*10^2k + (XlYr + XrYl)*10^k +XrYr.
That's four mpys, each 1/2 size of original. Multiplies by powers of 10 are just shifts, which with additions adds O(N) for the conquer phase.

Thus
T(N) = 4T(N/2)+O(N),
Which from our general recurrence theorem is O(N²). Darn -- we're right on the edge, and it's that constant of 4 that's the problem. But wait! Back to middle school...that 10^k term...?
(XlYr + XrYl) = (Xl-Xr)(Yr-Yl)+XlYl+XrYr.
So the LHS has 2 mpys and the RHS only 1 if we use XlYl and XrYr, already computed. Aha. That simplifies conquering by one mpy, so now we've got
T(N) = 3T(N/2)+O(N),
which by our general theorem means
T(N) = O(N raised to the log₂3) = O(N^1.59).

Weiss's Fig. 10.37 is a table showing the whole D&C algorithm on his example multiplication problem.

Matrix Multiplication

Really same story here: The basic 2-D subdivision idea,

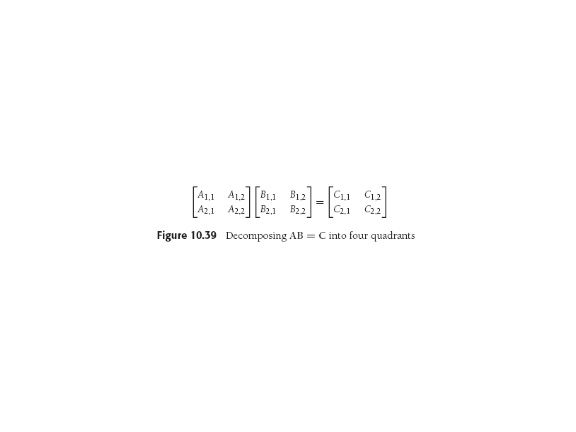
the matrix arithmetic, the obvious recurrence, the agony of defeat when it too yields exactly O(N³) because we need eight multiplies, the thrill of victory when by clever ordering of computations we (who's we? Strassen did all this and surprised everyone) go to seven *s, winding up with
T(N) = 7T(N/2)+O(N²),
Which is Big-Oh of N to the log₂7, or O(N^2.81).