Advanced Algorithms and Ideas

W. 9.4- 9.7

More pretty problems with practical, prosaic, profit-affecting power.

• Flows in Networks
• Minimum Spanning Tree (Prim, Kruskal)
• Depth First Search Applications
  • DFS algorithm (tree traversal) and definitions:
  • Undirected graphs: Biconnectivity
  • Undir: Euler paths and circuits, Hamiltonian cycles.
  • Directed: Strong components

Finally, 9.7 is NP Completeness.

So we're going to have to make some choices here.

Topological Sort Drive-by

A Topological sort is an ordering of vertices in DAG such that if there is a path from v to w in G, w appears after v in the order. Imagine course prerequisites. Not possible if graph has cycle. And not unique.

Idea: find vertex with no incoming edges (indegree 0). print it out, remove it and its edges. Repeat until done. Scanning the adjacency array repeatedly gives O(|V|²) time.

Faster is to keep the un-printed vertices of indegree 0 in a special spot so we don't have to hunt for them. Like a stack or queue. With adjacency lists, the main action of the algorithm is executed at most once per edge (code in Fig. 9.7). Need to get started by computing indegrees of all the nodes, which like the main algorithms is an O(|V|+|E|) calculation.

Shortest Path

Important (p. 366). Driving times, comms costs, etc. Generally, weighted graph (with costs on edges). Can solve unweighted SP on such a graph too.

Single-source Shortest Path Problem: given weighted G = (V,E) and distinguished vertex v, find the shortest weighted path from v to every other vertex in G.

If graph has a cycle with negative cost, shortest path isn't defined.

Upcoming: unweighted SP in O(|V|+|E|), then weighted no neg. edges in O(|E|log|V|). Simple but costly solution to negative edges, O(|E||V|). Acyclic graphs can be done in linear time.

Unweighted SP Drive-by

SP PPT

This is good place to get familiar with the bookkeeping that Weiss uses for these SP algorithms. It's a simple 4-column table that collects partial and final results, computed both from it and from a simple graph representation.

(vx, status, s-vx dist, prev vx.)

v  known dv   pv  
v1 T     0    0
v2 T     3    v1
v3 F    inf   0
...

Ch. 9.3 uses sequences of these tables to illustrate the computation.

BUT! The algorithms that use the tables are O(|V|²), and therefore considered bad. The problem is having to look thru all vertices to select one to work on: we'd like smarter "vertex selection", which we can get by using an ancillary data-structure like a queue or a priority queue. So:

(graph rep +) table sequence: good for understanding computation.
Augmented graph rep: good in more efficient data structures (queues, etc.) with better Big-Oh performance.

Reader's Guide: Figs 9.10-9.14 show SP calculation with an augmented graph (presumably array-list) represention. THEN the table is introduced and you get Fig. 9.16 for the algorithm code and Fig. 9.19 showing what happens to the table. THEN you're told "raw table means quadratic performance, don't do it", THEN you're shown the queue program in 9.18 which would produce the results of Figs. 9.10-9.14. (!!). This pattern is going to continue, so be ready.

As for top.sort, first effort is O(|V|²), and second makes clever use of a queue both to represent and keep separate two "boxes" of vertices of interest to be investigated next. As in top sort, similar algorithm and analysis: O(|V|+|E|), or linear.

Weiss asks in exercises: using a stack instead of a queue, can a different ordering arise? Why might one choice give a "better" answer?

Weighted SP: Dijkstra's Algorithm

Famous, elegant, and greedy. Make decisions using "nearby", locally-available information without searching or looking ahead. E.g. Hillclimbing, or gradient ascent, which works for some functions, not for others. If it works, no going back, no tiresome searching, efficient.

Designate vertex s. Just like unweighted SP, keep for each vertex its known-status, tentative distance to s, the last vertex added to path that caused change in the distance (note this will be the vertex preceding it in the (tentative and final) shortest path. The distance is the shortest path from s to v using only known vertices. An unknown vertex may offer a shorter path.

D's A. picks a vertex v with the smallest dv amongst all the unknown vertices, changes its status to known and updates its shortest path distance to s. That means that the tentative distances of its successors may have to be updated.

That is, for a vertex w adjacent to v, change its dw to dv + cost(v,w) if that's an improvement.

Dijkstra in I-MAX 3-D

You wish. Here's our graph: our s is v1.

Thinking of an evolving table with rows for
v status dv pv states. The first v1 is declared known, leaving v4 as the unknown-status vertex of minimum dv, so it is "known" next, and then we see:

Follow along on p. 375. Or one can pack everything into a graph movie using the augmented representation in which each vertex has status, distance-from-s, and previous-vertex information. Colours would be better (as in TP's PPTs). Here vertex names and edge costs are obvious. The small numbers by vertices are their tentative distances (dv's), the *'s are 'known' status.

SP PPT

Analysis: note edges with negative costs can cause wrong answers for the greedy algorithm, so we disallow them for now. Once again, sequential scanning of the adjacency list to find the minimum distance takes O(|V|) time for each vertex we consider, thus O(|V|²) time for the whole algorithm. Since there is at most one distance update per edge, we have O(|E| + |V|²). This is good, in fact linear, for a dense graph, which has O(|V|²) edges.

For the more usual sparse graphs, (|E| = Θ(|V|)), the same old objections, so we need a "box" to put vertices so we can.... pull out the smallest. So....?

Right, priority queue, and there are two different ways to use it:
1. selection of a vertex is clearly deleteMin(), and updating the tentative distances can be done with a decreaseKey() operation (Ch 6.3.4 -- change the key and percolate up). This gives O(|E|log|V|+ |V|log|V|)) = O(|E|log|V|). The location in the p-queue of each successor is found from the adjacency list of a vertex, and their distance d_i must be maintained and updated whenever d_i changes. Weiss says that a binary heap is not a good choice here, but a pairing heap (way ahead in Ch. 12) is better.

2. The second method is perhaps a bit uglier, leaving the queue full of old values that don't matter but do take up space. --- p. 378.

Negative Edge Cost SP

Weiss 9.3.3: Dijkstra fails: Despite negative costs being extremely rare in real problems, we academics of course and therefore consider negative costs a challenge. The problem is an unknown negative cost path can give shorter path to the "known" vertex. Fairly simple fix, but result is O(|V||E|). Neg. cost cycles can be detected.

Acyclic Graphs and Critical Paths

Weiss 9.3.4

With a DAG, the natural vertex selection goes in topologically-sorted order (Aha!). In fact, all necessary updates can be done as the sort goes on, so it's a one-pass process. Lots of real situations handled by DAGs; say you have activities (manufacturing, processing) that may depend on the completion of other activities.

Activity-node graph has dependence (arcs); vertex has cost (time) of the activity.

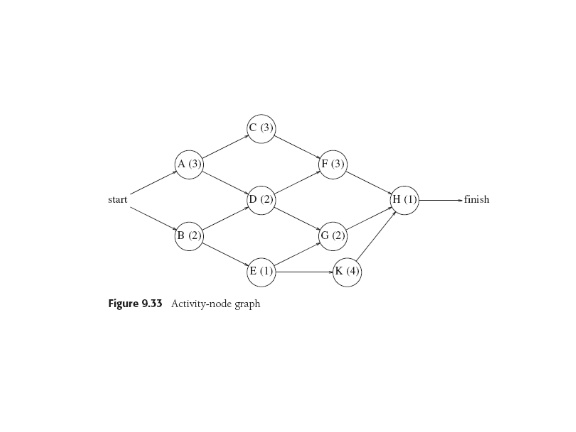
Computation uses an "event-node graph" easily made from the activity-node graph.

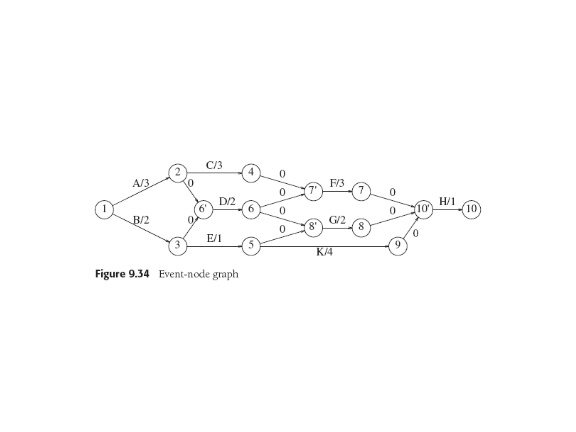
Relevant questions: What's earliest completion time? Given that, managers might want to know what activities can be delayed, and by how long, etc.

The earliest completion time is the longest path from first event to last event. Longest paths make sense here becuse our graphs are acyclic. Weiss gives Dijkstra-like formulae for EC and for LC, the latest time an event can finish without affecting final completion time. The slack time of an edge is the amount one can delay the corresponding activity without delaying overall completion time.

All Pairs Shortest Path

What it says. Could run Dijkstra's SSSP |V| times (best for sparse graphs). For dense graphs, there's a special version of the same approach that has tight loops and could beat D's Alg. Both are O(|V|³).